Оглавление
Характеристики простых линз[править]
В зависимости от форм различают собирающие (положительные) и рассеивающие (отрицательные) линзы. К группе собирательных линз обычно относят линзы, у которых середина толще их краёв, а к группе рассеивающих — линзы, края которых толще середины. Следует отметить, что это верно только если показатель преломления у материала линзы больше, чем у окружающей среды. Если показатель преломления линзы меньше, ситуация будет обратной. Например пузырёк воздуха в воде — двояковыпуклая рассеивающая линза.
Линзы характеризуются, как правило, своей оптической силой (измеряется в диоптриях), и фокусным расстоянием.
Для построения оптических приборов с исправленной оптической аберрацией (прежде всего — хроматической, обусловленной дисперсией света, — ахроматы и апохроматы) важны и иные свойства линз и их материалов, например, показатель преломления, коэффициент дисперсии, показатель поглощения и показатель рассеяния материала в выбранном оптическом диапазоне.
Иногда линзы/линзовые оптические системы (рефракторы) специально рассчитываются на использование в средах с относительно высоким показателем преломления (см. иммерсионный микроскоп, иммерсионные жидкости).
 Виды линз:Собирающие: 1 — двояковыпуклая 2 — плоско-выпуклая 3 — вогнуто-выпуклая (положительный(выпуклый) мениск)Рассеивающие: 4 — двояковогнутая 5 — плоско-вогнутая 6 — выпукло-вогнутая (отрицательный(вогнутый) мениск)
Виды линз:Собирающие: 1 — двояковыпуклая 2 — плоско-выпуклая 3 — вогнуто-выпуклая (положительный(выпуклый) мениск)Рассеивающие: 4 — двояковогнутая 5 — плоско-вогнутая 6 — выпукло-вогнутая (отрицательный(вогнутый) мениск)
Использование линзы для изменения формы волнового фронта. Здесь плоский волновой фронт становится сферическим при прохождении через линзу
Выпукло-вогнутая линза называется мениском и может быть собирательной (утолщается к середине), рассеивающей (утолщается к краям) или телескопической (фокусное расстояние равно бесконечности). Так, например линзы очков для близоруких — как правило, отрицательные мениски.
Вопреки распространённому заблуждению, оптическая сила мениска с одинаковыми радиусами не равно нулю, а положительна, и зависит от показателя преломления стекла и от толщины линзы. Мениск, центры кривизны поверхностей которого находятся в одной точке называется концентрической линзой (оптическая сила всегда отрицательна).
Отличительным свойством собирательной линзы является способность собирать падающие на её поверхность лучи в одной точке, расположенной по другую сторону линзы.

Основные элементы линзы: NN — оптическая ось — прямая линия, проходящая через центры сферических поверхностей, ограничивающих линзу; O — оптический центр — точка, которая у двояковыпуклых или двояковогнутых (с одинаковыми радиусами поверхностей) линз находится на оптической оси внутри линзы (в её центре).Примечание. Ход лучей показан, как в идеализированной (тонкой) линзе, без указания на преломление на реальной границе раздела сред. Дополнительно показан несколько утрированный образ двояковыпуклой линзы.
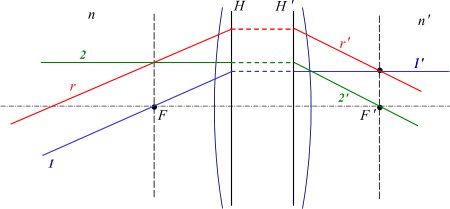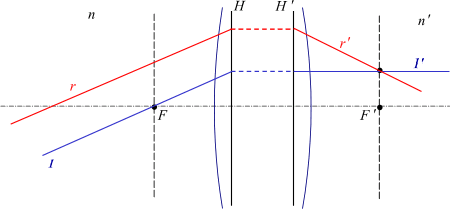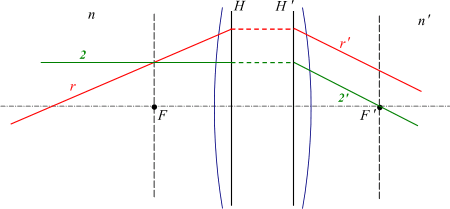
Если на некотором расстоянии перед собирательной линзой поместить светящуюся точку S, то луч света, направленный по оси, пройдёт через линзу не преломившись, а лучи, проходящие не через центр, будут преломляться в сторону оптической оси и пересекутся на ней в некоторой точке F, которая и будет изображением точки S. Эта точка носит название сопряжённого фокуса, или просто фокуса.
Если на линзу будет падать свет от очень удалённого источника, лучи которого можно представить идущими параллельным пучком, то по выходе из неё лучи преломятся под бо́льшим углом и точка F переместится на оптической оси ближе к линзе. При данных условиях точка пересечения лучей, вышедших из линзы, называется фокусом F’, а расстояние от центра линзы до фокуса ОF’ — фокусным расстоянием.
Лучи, падающие на рассеивающую линзу, по выходе из неё будут преломляться в сторону краёв линзы, то есть рассеиваться. Если эти лучи продолжить в обратном направлении так, как показано на рисунке пунктирной линией, то они сойдутся в одной точке F, которая и будет фокусом этой линзы. Этот фокус будет мнимым.

Мнимый фокус рассеивающей линзы

Мнимый фокус F точки S на оси N-N рассеивающей линзы
Сказанное о фокусе на оптической оси в равной степени относится и к тем случаям, когда изображение точки находится на наклонной линии, проходящей через центр линзы под углом к оптической оси. Плоскость, перпендикулярная оптической оси, расположенная в фокусе линзы, называется фокальной плоскостью.
Собирательные линзы могут быть направлены к предмету любой стороной, вследствие чего лучи по прохождении через линзу могут собираться как с одной, так и с другой её стороны. Таким образом, линза имеет два фокуса — передний и задний. Расположены они на оптической оси по обе стороны линзы на фокусном расстоянии от главных точек линзы.
Дифракционная решетка
Дифракционная решетка – это оптический прибор, предназначенный для наблюдения дифракции света.
Дифракционная решетка представляет собой систему параллельных щелей равной ширины, лежащих в одной плоскости и разделенных равными по ширине непрозрачными промежутками.
Дифракционную решетку применяют для разложения света в спектр и измерения длин световых волн.
Период решетки – это величина, равная сумме ширины прозрачной и непрозрачной полос решетки.
Обозначение – \( d \), единица измерения в СИ – м.
где \( a \) – ширина прозрачной полосы; \( b \) – ширина непрозрачной полосы.
Если решетка регулярна, т. е. ее прозрачные и непрозрачные полосы имеют одинаковую ширину, то период решетки можно рассчитать, разделив ее длину на число штрихов:
где \( l \) – длина решетки, \( N \) – число штрихов.
Формула дифракционной решетки
где \( d \) – период решетки; \( \varphi \) – угол дифракции; \( k \) = 0; 1; 2… – порядок максимума, считая от центрального \( k \) = 0 и расположенного напротив центра решетки; \( \lambda \) – длина волны, падающей на решетку нормально к ней.

Если дифракционная решетка освещается белым светом, то при \( k \) ≠ 0 разным длинам волн будут соответствовать разные дифракционные углы. Поэтому положение главных максимумов ненулевого порядка будет различным. Центральный максимум (\( k \) = 0) остается белым, т. к. при \( k \) = 0 для всех длин волн \( \varphi \) = 0, т. е. положение главного максимума для всех длин волн одинаково. Все остальные максимумы имеют вид радужных полос, называемых дифракционными спектрами первого порядка (\( k \) = 1), второго порядка (\( k \) = 2) и т. д. Ближе к центральному максимуму находится фиолетовый край спектра, дальше всего – красный, т. к. \( \lambda_{фиол}<\lambda_{кр} \), то и \( \varphi_{фиол}<\varphi_{кр} \).
Важно! Поскольку углы, под которыми наблюдаются максимумы первого и второго порядка, не превышают 5°, можно вместо синусов углов использовать их тангенсы
Линзы по покрытиям
Практически все полимерные линзы (да и некоторая часть стеклянных) имеют различные покрытия.
Очковые линзы разных типов, ценовых категорий и разных производителей снабжаются покрытиями, разных химических составов, физических характеристик и в разных комбинациях. Хотя сложность этого многообразия кажущаяся. Все современные виды покрытий обладают схожими свойствами
Важно различать их типы и то, как эти покрытия меняют потребительские свойства линзы. Ну и важно понимать также, что покрытия линз наиболее передовых и успешных компаний, использующих свои новейшие разработки, по определению превосходят по качественным характеристикам более дешёвые аналоги
По типам покрытия линз разделяют на:
- упрочняющие покрытия — пленки, наносимые на поверхности линзы с целью воспрепятствования появлению царапин (абразивостойкость). Дело в том, что полимерные линзы гораздо больше, чем стеклянные подвержены появлению царапин. Подобные покрытия препятствуют этому и могут существенно продлить срок службы линз;
- просветляющие покрытия – как правило, серия пленок (до десяти), состав и, главное, толщина которых должны быть выдержаны в очень строгих пределах. Назначение просветляющего покрытия — снизить количество отражённого света от поверхности линзы. Ещё такие покрытия называют антибликовыми (блик, это и есть отражённый свет). Можно добавить, что качественные линзы с такими покрытиями гораздо меньше заметны на лице;
- антистатическое покрытие – плёнка, препятствующая накоплению статического заряда на поверхности линзы, из-за которого к ней пристают электрически заряженные частички пыли. От этого линза загрязняется и при протирке эти частички пыли царапают поверхность линзы;
- водо и грязеотталкивающее покрытие – плёнка, препятствующая смачиванию поверхности линзы. Такое покрытие ещё называют гидрофобным (дословно означает водобоязнь). Благодаря ему частички воды не расплываются по поверхности линзы, а сбираются в крупные капли, которые легко удалить или они стекают сами, не оставляя следа. Кроме того на линзе с таким покрытием остается гораздо меньше следов от пальцев.
Неправильно было бы считать, что плёнки на линзах делают её полностью защищённой от агрессивных факторов. Но, тем не менее, современные покрытия реально улучшают потребительские свойства линз, иногда в разы продляя срок их службы и повышая комфорт их использования. Именно поэтому сегодня невозможно встретить дорогие качественные линзы без специальных мультипокрытий.
Линзы без покрытия
Линзы без покрытий — это обычные линзы экономичного ценового диапазона.
Кроме того, если Вы предпочитаете придать себе неповторимый облик, окрасив линзы Ваших очков в оригинальный цвет, Вы должны остановить свой выбор именно на линзах без покрытия.
При этом следует понимать, что полимерные линзы без специальных покрытий царапаются гораздо легче. Да и остальные потребительские характеристики необработанных линз будут существенно ниже.
Главным недостатком, пожалуй, можно считать высокую подверженность царапанию, особенно усиленную электростатическим эффектом, провоцирующим налипание абразивной пыли на поверхности линзы.
Следом идёт отсутствие просветляющих покрытий. При прохождении сквозь очковую линзу часть света отражается от ее поверхностей. Это приводит к возникновению мешающих отражений и снижению четкости восприятия изображения.

Ну и в довершение, линзы без покрытий в гораздо большей степени подвержены загрязнениям (от влаги и воды, от пальцев, от жировых и потовых отложений, осаждающихся на линзе в процессе эксплуатации очков).
В результате срок службы таких линз оказывается иногда в разы короче линз со специальными покрытиями.

Линзы по типу
По типу очковые линзы можно разделить на:
- однофокальные – то есть имеющие один фокус (одну диоптрию);
- мультифокальные – сложные по форме линзы, имеющие несколько фокусов (три и два соответственно).
Если у Вас близорукость (миопия) или дальнозоркость (гиперметропия), с астигматизмом или без – не важно, то Вам нужны обычные монофокальные линзы. Если у Вас пресбиопия (в основном это имеет место после 40 лет), то есть ухудшение Вашего зрения связано с возрастом (аккомодация глаза уменьшается и связано это с уменьшением эластичности хрусталика), то Вам могут понадобиться мультифокальные линзы, которые, в свою очередь подразделяются на:
Если у Вас пресбиопия (в основном это имеет место после 40 лет), то есть ухудшение Вашего зрения связано с возрастом (аккомодация глаза уменьшается и связано это с уменьшением эластичности хрусталика), то Вам могут понадобиться мультифокальные линзы, которые, в свою очередь подразделяются на:
- бифокальные;
- прогрессивные;
- офисные.
Бифокальные линзы
Бифокальные линзы позволяют скомпенсировать сразу два дефекта зрения. Такие линзы предназначены для чёткого видения на больших расстояниях и одновременно, позволяют различать близко расположенные предметы благодаря специальному сектору в нижней части линзы. Это позволяет заменить двое очков: «для дали» и «для чтения»
Важной особенностью является то, что правая и левая линза не взаимозаменяемы

Прогрессивные линзы
Прогрессивные линзы (ещё их называют вариофокальными) — это более современные и совершенные линзы, во многом аналогичные бифокальным, но не имеющие чётко выраженных зон для разных расстояний. За счёт этого внешне они ничем не отличаются от обычных линз. Позволяют заменить двое очков: «для дали» и «для чтения». Кроме этого, имеют переходную зону оптического действия (коридор прогрессии). В результате такой сложный дизайн линзы помогает обеспечить чёткое видение во всём диапазоне необходимых расстояний даже для глаз с ослабленной аккомодацией (когда пациент не способен чётко различать предметы и вблизи и вдали)
Важной особенностью является то, что правая и левая линза не взаимозаменяемы
В периферийных зонах, расположенных справа и слева от коридора прогрессии пациент может наблюдать искажения, избавиться от которых невозможно. Однако в современных прогрессивных линзах эти искажения настолько минимизированы, что замечаются, обычно, только в начальный период адаптации к новой линзе.

Офисные линзы
Офисные линзы являются частным случаем прогрессивных линз, но предназначены для коррекции зрения на ближних (чтение, работа с документами) и средних расстояниях (компьютер, офис). От прогрессивных линз они отличаются тем, что не содержат зону для дали (предполагается, что зрение вдаль в подобных случаях не нуждается в коррекции). За счёт этого зоны, обеспечивающие чёткое видение, по сравнению с прогрессивными линзами существенно расширены.
При этом они обладают важным преимуществом перед обычными линзами для близи (для чтения). Дело в том, что линзы для близи предназначены для расстояний около 40 см. Однако в реальной жизни гораздо чаще приходится постоянно переводить взгляд с одних расстояний на другие. Прежде всего, это работа на компьютере, когда взгляд должен фокусироваться то на документах, то на клавиатуре, то на экране монитора и так десятки и сотни раз в течение дня. Добавьте сюда необходимость периодически отвлекаться на собеседника, и станет понятно, что нагрузка для глаз получается запредельной.
Врачи-офтальмологи давно заметили, что у пациентов с пресбиопией, раньше перешедших на мультифокальные линзы (офисные или прогрессивные), естественные процессы ослабления зрения, связанные с возрастом, протекают ощутимо медленнее.
Офисные линзы также относятся к классу мультифокальных, однако, в силу того, что они предназначены для коррекции зрения на ближних и средних расстояниях, основной рефракцией в них принято считать оптическую силу для близи, а уменьшение рефракции в зоне, для средних расстояний обозначать через дегрессию (или уменьшение).
Как следует из названия, очки с такими линзами предназначены для помещений (офиса или дома). Использовать их вне помещений (на улице, за рулём автомобиля) не рекомендуется, поскольку они не предусматривают чёткого видения предметов на больших расстояниях.

Линзы со специальными свойствами[править]
Линзы из органических полимеровправить
Полимеры дают возможность создавать недорогие асферические линзы с помощью литья.
Линзы контактные
В области офтальмологии созданы мягкие контактные линзы. Их производство основано на применении материалов, имеющих бифазную природу, сочетающих фрагменты кремний-органического или кремний-фторорганического полимера силикона и гидрофильного полимера гидрогеля. Значительных результатов в этом направлении достигли зарубежные фирмы Ciba Vision (Швейцария) и Bausch & Lomb (США). Работа в течении более 20 лет привела к созданию в конце 90-х годов силикон-гидрогелевых линз, которые благодаря сочетанию гидрофильных свойств и высокой кислородопроницаемости могут непрерывно использоваться в течение 30 дней круглосуточно.
Линзы из кварцаправить
- Основная статья: Линзы из кварца
Оптический кварц (Кварцевое стекло) находит широкое применение в Оптических системах (ОС) обладает рядом полезных оптических свойств. Кварцевое стекло — переплавленный чистый кремнезём с незначительными (около 0,01 %) добавками Аl2О3, СаО и MgO. Оно отличается высокой термостойкостью и инертностью ко многим химическим реактивам за исключением плавиковой и фосфорной кислот.
Прозрачное кварцевое стекло хорошо пропускает ультрафиолетовые и видимые лучи света. Широкое внедрение кварцевого стекла в практику начато в России благодаря новым технологиям получения оптических элементов из кремния и кварца, созданию производства для изготовления и обработки этих оптических материалов.
Линзы из кремнияправить
- Основная статья: Рентгеновская оптика преломления

Линза преломления ретгеновских лучей

Рис.1. Схема преломления X-лучей.
Линзы из кремния или рентгеновская оптика преломления — линзы, изготовленные из однородного кремния, прозрачные для инфракрасного излучения, рентгеновсого излучения, преломляющие Х-лучи
В настоящее время нашли применение линзы из кремния
Это связано с современным уровнем технологий обработки твёрдых кристаллов и самое важное, кремний сочетает сверхнизкую! дисперсию с самым большим абсолютным значением коэффициента преломления n=3,4! в диапазоне ИК-излучения; линзы из кремния прозрачны к Х-лучам и способны их преломлять, фокусировать (мягкие и жёсткие Х-лучи), что в последнее время находят широкое применение в микроскопии, телескопии, вытесняя рентгеновскую дорогостоящую оптику с применением зеркал и оптических систем «скользящего» преломления Х-лучей. Они полностью непрозрачны в видимом диапазоне спектра
Кроме этого кремний обладает способностью создавать материалы, имеющих бифазную природу, сочетающих фрагменты кремний-органического или кремний-фторорганического полимера силикона и гидрофильного полимера гидрогеля. Что делает его самым перспективным в изготовлении мягких контактных линз.
П2.1. Вычисление и отображение параксиальных характеристик положительной линзы
Рассмотрим последовательность действий для нахождения оптической системы на примере.
Оптические системы принято задавать радиусами кривизны поверхностей (нумерация
поверхностей ведется по ходу луча), расстояниями между поверхностями,
которые откладываются вдоль оптической оси и показателями преломления
сред, находящимися между поверхностями (линз или воздушных промежутков).
Пусть у нас задана оптическая система в воздухе со следующими
параметрами:
П2.1.1. Вычисление параксиальных характеристик положительной
линзы
Для того чтобы найти параксиальные характеристики системы, необходимо
вычислить ее ,
которая определяется как последовательное перемножение матриц
и всех элементов
оптической системы.
Нахождение матриц преломления и переноса
Матрица преломления оптической поверхности выглядит следующим образом:
,
где —
кривизна поверхности, ,
— показатели преломления до и после поверхности.
Матрица переноса от одной поверхности до другой выглядит следующим образом:,
где —
приведенное расстояние между оптическими поверхностями.
|
Матрицы преломления для данной оптической системы будут выглядеть , Матрица переноса между поверхностями будет такая: |
Нахождение матрицы преобразования
Матрица преобразования оптической системы, состоящей из нескольких компонентов,
разделенных промежутками, будет состоять из произведения матриц преломления
и матриц переноса для
отдельных компонентов:
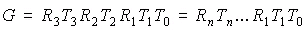
Вычисление параксиальных характеристик
Зная значение элементов матрицы преобразования оптической системы, можно
определить значения параксиальных характеристик:
П2.1.2. Отображение параксиальных характеристик
положительной линзы
В соответствии с , все положительные отрезки откладываются слева направо, а отрицательные
— справа налево.
Отображение вершинных отрезков
Отложим (в соответствии с правилом знаков) передний и задний вершинные
отрезки и найдем .
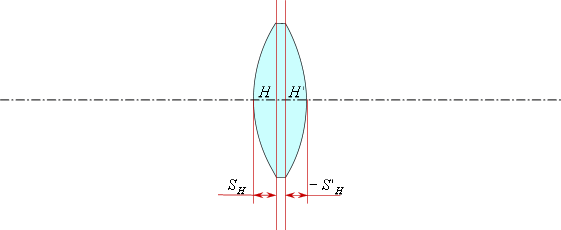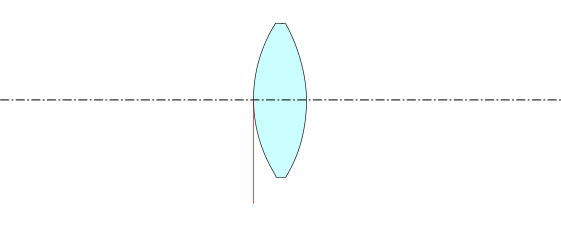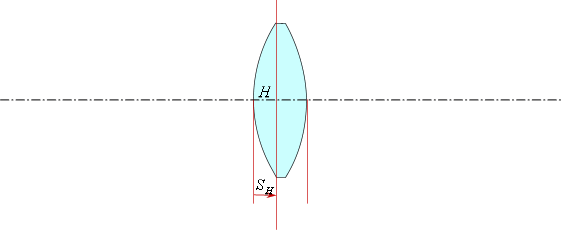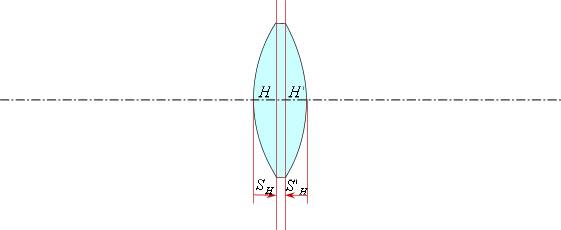
Передний вершинный отрезок
— это расстояние от первой поверхности до передней главной плоскости.Задний вершинный отрезок
— это расстояние от последней поверхности до задней главной плоскости.
В данном случае передний вершинный отрезок —
положительный, следовательно, откладываем от первой поверхности вправо.
Задний вершинный отрезок —
отрицательный, следовательно, откладываем его от последней поверхности
влево.
Отображение фокальных отрезков
Теперь отложим
и фокальные отрезки
и найдем положение фокусов.
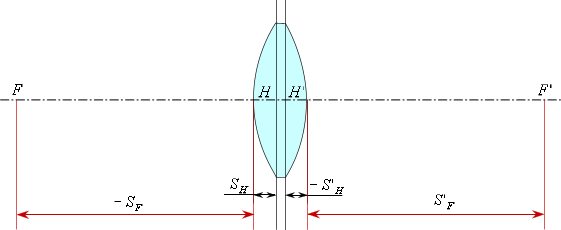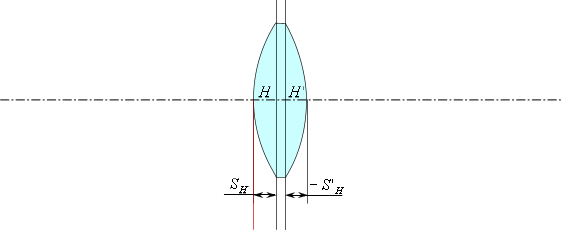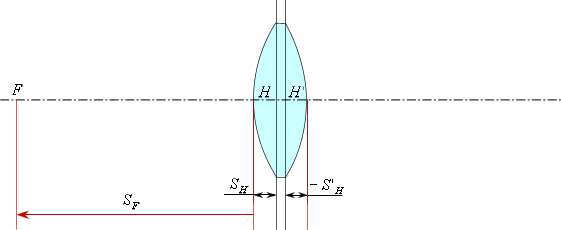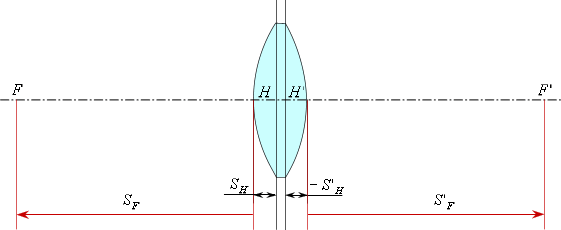
Передний фокальный отрезок —
это расстояние от первой поверхности до . Задний фокальный отрезок
— это расстояние от последней поверхности до .
В данном случае передний фокальный отрезок
— отрицательный, следовательно, откладываем его от первой поверхности
влево. Задний фокальный отрезок
— положительный, следовательно, откладываем его от последней поверхности
вправо.
Отображение фокусных расстояний
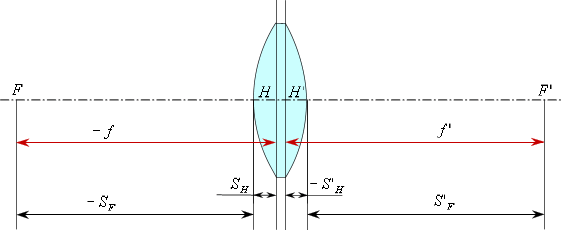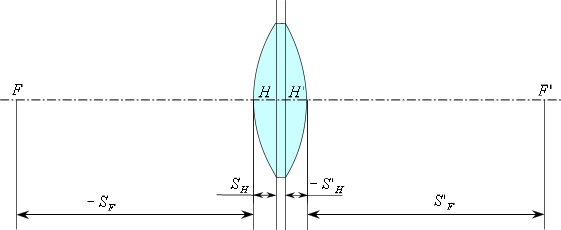
Переднее фокусное расстояние
— это расстояние от передней до переднего фокуса.Заднее фокусное расстояние —
это расстояние от задней главной точки до заднего фокуса.
В данном случае переднее фокусное расстояние
— отрицательное, следовательно, откладываем его от передней главной точки
влево. Заднее фокусное расстояние
— положительное, следовательно, откладываем его от задней главной точки
вправо.
5.2. Теория идеальных оптических систем (параксиальная или гауссова оптика)
5.2.1. Основные положения
В параксиальной области (бесконечно близко к ), любая реальная система ведет себя как идеальная:
Каждой точке пространства предметов можно поставить
в соответствие в пространстве изображений.
Каждая прямая линия имеет в пространстве изображений.
Каждая плоскость пространства предметов имеет
сопряженную ей плоскость в пространстве изображений.
Из этих положений следует, что:
имеет сопряженную ей меридиональную плоскость в пространстве
изображений.
Плоскость в пространстве предметов, перпендикулярная
оптической оси, имеет сопряженную ей плоскость, перпендикулярную оптической
оси в пространстве изображений.
5.2.2. Линейное, угловое, продольное
увеличение
Линейное (поперечное) увеличение
Линейное
увеличение оптической системы – это отношение линейного размера изображения
в направлении, перпендикулярном оптической оси, к соответствующему размеру
предмета в направлении перпендикулярном оптической оси:
|
|
Для линейное увеличение для любой величины предмета
и изображения в одних и тех же плоскостях одно и то же.
Угловое увеличение
Угловое увеличение оптической системы – это
отношение тангенса угла между лучом и оптической осью в пространстве изображений
к тангенсу угла между сопряженным с ним лучом в пространстве предметов и
осью:
|
|
В параксиальной области углы малы, и следовательно, угловое
увеличение – это отношение любых из следующих угловых величин:
Продольное увеличение
Продольное увеличение оптической
системы – это отношение бесконечно малого отрезка, взятого вдоль оптической
оси в пространстве изображений, к сопряженному с ним отрезку в пространстве
предметов:
|
|
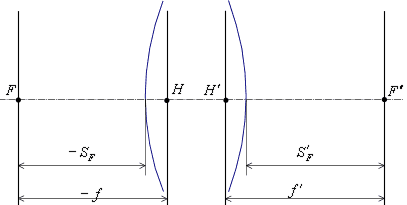
5.2.3. Кардинальные точки и отрезки
Главными плоскостями системы
называется пара сопряженных плоскостей, в которых линейное увеличение
равно единице ().
|
Главные точки Задний фокус – Расстояние от задней главной Расстояние от последней |
 |
Передняя (задняя) фокальная
плоскость — плоскость, перпендикулярная
оптической оси и проходящая через передний (задний) фокус.
Передний фокус
– это точка на оптической оси в пространстве предметов, сопряженная с
бесконечно удаленной точкой, расположенной на оптической оси в пространстве
изображений
Если лучи выходят из переднего фокуса, то они идут в
пространстве изображений параллельно.
Переднее фокусное расстояние
– это
расстояние от передней главной точки до переднего фокуса.
Передний фокальный отрезок
– это
расстояние от первой поверхности до переднего фокуса.
Если ,
то система называется собирающей или положительной. Если
, то система
рассеивающая или отрицательная.
Переднее и заднее фокусные расстояния
связаны между собой соотношением или
, где
– приведенное
или эквивалентное фокусное расстояние.
В том случае, если оптическая система находится в однородной
среде (например, в воздухе) ,
следовательно, переднее и заднее фокусные расстояния равны по абсолютной
величине .
|
|
5.2.4. Построение изображений
Построение изображения:
| Для того чтобы найти изображение точки , необходимо построить хотя бы два вспомогательных луча, на пересечении которых и будет находиться точка . Вспомогательный луч можно провести через точку параллельно оптической оси, тогда в пространстве изображений луч пройдет через задний фокус оптической системы. Вспомогательный луч можно провести через точку и передний фокус оптической системы, тогда в пространстве изображений луч пойдет параллельно оптической оси. На пересечении лучей и будет находиться изображение точки . |
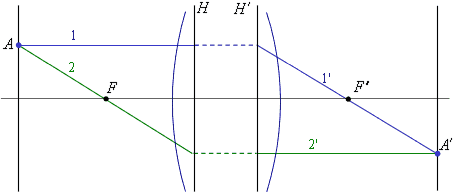 |
Построение хода луча :
|
1 способ. Можно построить вспомогательный 2 способ. Можно построить вспомогательный |
|
Примеры решения задач
Пример 1
Задача
Задан эллипс уравнением
и точки
. Необходимо:
- убедиться, что точки
и
лежат на эллипсе; - найти полуоси эллипса и координаты его фокусов;
- найти расстояние от точки
к фокусам; - убедиться, что сумма этих расстояний равна длине большой оси;
- найти эксентриситет эллипса.
Решение
1. Подставим координаты
точки
в левую часть уравнения эллипса:
– точка
лежит на эллипсе. Аналогично для
:
точка
лежит на эллипсе.
2. С канонического
и данного уравнения
эллипса выходит:
Из равенства
получается:
– полуфокусное расстояние. Координаты фокусов
и
.
3. Найдём фокальные радиусы точки
4. Найдём сумму
, что отвечает определению эллипса.
5. Эксцентриситет находится по формуле
.
Пример 2
Задача
Найти оси, вершины и фокусы эллипса
Решение
Сведём обычное уравнение к каноническому:
,
. Вершины эллипса в точках
,
,
,
. Строим вершины на координатных осях и соединяем плавной линией (см. рис. 2). Так как в данном случае
больше, чем
, то эллипс, который вытянут вдоль оси
, находим полуфокусное расстояние
.
Фокусы в точках
и
. (см. рис. 3)
Рис. 4
Пример 3
Найти оси, вершины и фокусы эллипса
или
. Построить эллипс.
Сравнивая последнее уравнение с уравнением (2), у нас получается:
,
. Откуда находим оси эллипса:
,
и координаты вершин:
,
,
,
. Дальше из формулы:
. Значит, фокусами эллипса есть точки:
и
. Для построения эллипса отложим на осях
и
вершины
соответственно соединим их плавной линией, (см. задачу 1).
Замечание! Если в каноническом уравнении
большей полуосью будет
, тогда фокусы эллипса будут расположены на оси
и тогда
.

Эта тема закрыта для публикации ответов.